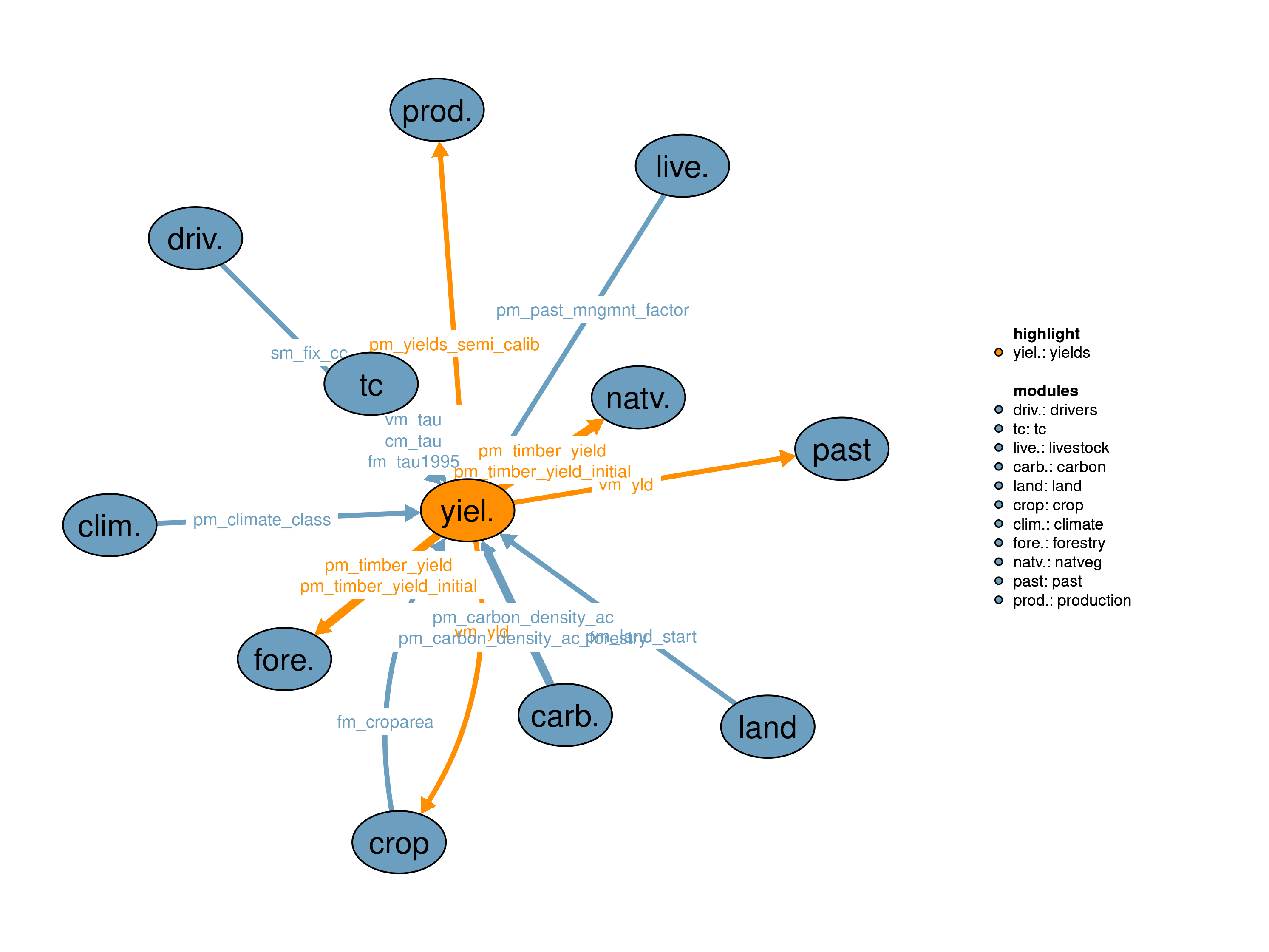
The yields module simulates the temporal development of crop yields and pasture productivity. Spatially explicit information on pasture productivity and crop yields under both rainfed and irrigated conditions is provided by the global gridded crop model LPJmL (Lund-Potsdam-Jena with managed Land) (Bondeau et al. 2007). In the initial year of the simulation period, crop yields and pasture productivity are calibrated at the regional level to meet the observed cropland and pasture area as reported by FAO (FAOSTAT 2016). For the simulation of the temporal development of agricultural yields, the module receives information about the agricultural land use intensity represented by the \(\tau\) factor coming from the module 13_tc. Irrigated yields can optionally be calibrated to meet irrigated-rainfed country-level yield ratios as reported by Aquastat (FAO 2016).
The module returns yields for all crops and for pasture, which is then used by the modules 30_crop and 31_past.
| Description | Unit | A | |
|---|---|---|---|
| fm_croparea (t_all, j, w, kcr) |
Different croparea type areas | \(10^6 ha\) | x |
| fm_tau1995 (h) |
Agricultural land use intensity tau in 1995 | \(1\) | x |
| pcm_tau (h, tautype) |
Tau factor of the previous time step | \(1\) | x |
| pm_carbon_density_ac (t_all, j, ac, ag_pools) |
Above ground natveg carbon density for age classes and carbon pools | \(tC/ha\) | x |
| pm_carbon_density_ac_forestry (t_all, j, ac, ag_pools) |
Above ground plantation carbon density for age classes and carbon pools | \(tC/ha\) | x |
| pm_climate_class (j, clcl) |
Koeppen-Geiger climate classification on the simulation cluster level | \(1\) | x |
| pm_land_start (j, land) |
Land initialization area | \(10^6 ha\) | x |
| pm_past_mngmnt_factor (t, i) |
Regional pasture management intensification factor | \(1\) | x |
| sm_fix_cc | year until which all parameters affected by cc are fixed to historical values | \(year\) | x |
| vm_tau (h, tautype) |
Agricultural land use intensity tau | \(1\) | x |
| Description | Unit | |
|---|---|---|
| pm_timber_yield (t, j, ac, forest_land) |
Forest growing stock | \(tDM/ha/yr\) |
| pm_timber_yield_initial (j, ac, forest_land) |
Initial Forest yield | \(tDM/ha/yr\) |
| pm_yields_semi_calib (j, kve, w) |
Potential yields calibrated to FAO regional levels | \(tDM/ha/yr\) |
| vm_yld (j, kve, w) |
Yields (variable because of technical change) | \(tDM/ha/yr\) |
The managementcalib_aug19 realization reads in the LPJmL data and performs a number of calibrations. First, a bioenergy yield correction is performed. As there is currently no robust information on bioenergy yields available in (FAOSTAT 2016), it is assumed that the LPJmL yields for bioenergy correspond to the yields achieved under the highest currently observed value of the \(\tau\) factor representing agricultural land-use intensity. Secondly, pasture yields are calculated based on pasture demand to account for in- and extensification of managed grasslands. Thirdly, irrigated yields are scaled to meet the irrigated-to-rainfed yield ratio as provided by AQUASTAT (FAO 2016). Finally, crop yields are calibrated to FAO (FAOSTAT 2016) regional yield levels of the initial time step. An additional feature of this realization is to allow crop yields technological change from the precedent times step to spillover to pasture areas. This realization also calculates the growth stocks in commercial plantations and natural vegetation using LPJmL Carbon stocks.
Technological change can increase the initial calibrated yields by:
\[\begin{multline*} vm\_yld(j2,kcr,w) = \sum_{ct}i14\_yields\_calib(ct,j2,kcr,w) \cdot \sum_{cell(i2,j2), supreg(h2,i2)}\left(\frac{ vm\_tau(h2,"crop") }{ fm\_tau1995(h2)}\right) \end{multline*}\]
For the current time step of the optimization, cellular yields of irrigated and rainfed crops are calculated by multiplying calibrated input yields from LPJmL with the intensification rate relative to the initial time step 1995. In the case of pasture yields, technological change cannot be fully translated into yield increases, to address that, an exogenous pasture management factor pm_past_mngmnt_factor is used to scale pasture yields based on the number of cattle reared to fulfill the domestic demand for ruminant livestock products in module 70.
Additionally, the parameter s14_yld_past_switch can be used to capture a certain magnitude of spillovers of the yield increase due to technological change from the time step before. It can range from 0 (no spillover) to 1 (full spillover).
\[\begin{multline*} vm\_yld(j2,"pasture",w) = \sum_{ct}\left(i14\_yields\_calib(ct,j2,"pasture",w) \cdot \sum_{cell(i2,j2)}pm\_past\_mngmnt\_factor(ct,i2)\right) \cdot \left(1 + s14\_yld\_past\_switch \cdot \left(\sum_{cell(i2,j2), supreg(h2,i2)}\left(\frac{ pcm\_tau\left(h2, "crop"\right)}{fm\_tau1995(h2)}\right) - 1\right)\right) \end{multline*}\]
The following equations calibrate the cellular yield patterns (f14_yields) to match FAO historical yields (f14_fao_yields_hist) by calculating a calibration term called ‘i14_managementcalib’. For most cases, ‘i14_managementcalib’ is the ratio of the historical yields reported by FAO (f14_fao_yields_hist) and regional mean yields (i14_modeled_yields_hist) given historic crop area patterns (‘fm_croparea’) and cellular yields coming from crop models like LPJmL (f14_yields). In these cases, ‘i14_managementcalib’ represents a purely relative calibration factor that depends only on the initial conditions of the starting year.
However, when FAO yields are significantly higher than given by the cellular yield inputs (underestimated baseline), the relative calibration terms can lead to unrealistically large yields in the case of future yield increases within the cellular yield patterns.
To address this issue, the factor i14_lambda_yields determines the degree to which the baseline (FAO) is under- or overestimated and therefore controls whether the calibration factor is applied as an absolute or relative change. For overestimated FAO yields, i14_lambda_yields is 1, which is equivalent to an entirely relative calibration. For underestimated yields, i14_lambda_yields is calculated as the squared root of the ratio between LPJmL yields and FAO historical yields, and as i14_lambda_yields approaches 0, it reduces the applied relative change resulting in a mean change increasingly similar to an additive term (Heinke et al. (2013)). This concept is referred to as limited calibration, as it limits the calibration to an additive term in case of a strongly underestimated baseline. The scalar s14_limit_calib can be used to switch limited calibration on (1) and off (0).
i14_croparea_total(t_all,w,j) = sum(kcr, fm_croparea(t_all,j,w,kcr));Historic crop area patterns (fm_croprea) are used to calculate regional yields (i14_modeled_yields_hist) from the given cellular input pattern. In rare cases where a region has no crop area reported for a given crop type, the total crop area is used to calculate a proxy yield for the calibration, given by the following equation:
i14_modeled_yields_hist(t_past,i,knbe14)
= (sum((cell(i,j),w), fm_croparea(t_past,j,w,knbe14) * f14_yields(t_past,j,knbe14,w)) /
sum((cell(i,j),w), fm_croparea(t_past,j,w,knbe14)))$(sum((cell(i,j),w), fm_croparea(t_past,j,w,knbe14))>0)
+ (sum((cell(i,j),w), i14_croparea_total(t_past,w,j) * f14_yields(t_past,j,knbe14,w)) /
sum((cell(i,j),w), i14_croparea_total(t_past,w,j)))$(sum((cell(i,j),w), fm_croparea(t_past,j,w,knbe14))=0);The factor i14_lambda_yields is calculated for the initial time step depending on the setting s14_limit_calib and is then held constant for all other time steps. The regional FAO yield and regional yield of the crop model input of the initial time step is kept constant in the two parameters i14_fao_yields_hist and i14_modeled_yields_hist:
loop(t,
if(sum(sameas(t,"y1995"),1)=1,
if ((s14_limit_calib = 0),
i14_lambda_yields(t,i,knbe14) = 1;
Elseif (s14_limit_calib =1 ),
i14_lambda_yields(t,i,knbe14) =
1$(f14_fao_yields_hist(t,i,knbe14) <= i14_modeled_yields_hist(t,i,knbe14))
+ sqrt(i14_modeled_yields_hist(t,i,knbe14)/f14_fao_yields_hist(t,i,knbe14))$
(f14_fao_yields_hist(t,i,knbe14) > i14_modeled_yields_hist(t,i,knbe14));
);
i14_fao_yields_hist(t,i,knbe14) = f14_fao_yields_hist(t,i,knbe14);
Else
i14_modeled_yields_hist(t,i,knbe14) = i14_modeled_yields_hist(t-1,i,knbe14);
i14_FAO_yields_hist(t,i,knbe14) = i14_fao_yields_hist(t-1,i,knbe14);
i14_lambda_yields(t,i,knbe14) = i14_lambda_yields(t-1,i,knbe14);
);
);The calibrated cellular yield i14_yields_calib is calculated for each time step depending on the constant values i14_modeled_yields_hist, i14_fao_yields_hist, i14_lambda_yields and the uncalibrated, cellular yield f14_yields following the idea of eq. (9) in (Heinke et al. 2013):
i14_managementcalib(t,j,knbe14,w) =
1 + (sum(cell(i,j), i14_fao_yields_hist(t,i,knbe14) - i14_modeled_yields_hist(t,i,knbe14)) /
f14_yields(t,j,knbe14,w) *
(f14_yields(t,j,knbe14,w) / (sum(cell(i,j),i14_modeled_yields_hist(t,i,knbe14))+10**(-8))) **
sum(cell(i,j),i14_lambda_yields(t,i,knbe14)))$(f14_yields(t,j,knbe14,w)>0);
i14_yields_calib(t,j,knbe14,w) = i14_managementcalib(t,j,knbe14,w) * f14_yields(t,j,knbe14,w);
pm_yields_semi_calib(j,knbe14,w) = i14_yields_calib("y1995",j,knbe14,w);Note that the calculation is split into two parts for better readability. Irrigated yields are calibrated to meet the country-level ratio between irrigated and rainfed yields reported by Aquastat. This can be de-activated with the switch s14_calib_ir2rf.
if ((s14_calib_ir2rf = 1),
i14_calib_yields_hist(i,w)
= sum((cell(i,j), knbe14), fm_croparea("y1995",j,"irrigated",knbe14) * i14_yields_calib("y1995",j,knbe14,w)) /
sum((cell(i,j), knbe14), fm_croparea("y1995",j,"irrigated",knbe14));
i14_calib_yields_ratio(i) = i14_calib_yields_hist(i,"irrigated") / i14_calib_yields_hist(i,"rainfed");
i14_target_ratio(i) = max(i14_calib_yields_ratio(i), f14_ir2rf_ratio(i));
i14_yields_calib(t,j,knbe14,"irrigated") = sum((cell(i,j)), i14_target_ratio(i) / i14_calib_yields_ratio(i)) *
i14_yields_calib(t,j,knbe14,"irrigated");
i14_modeled_yields_hist2(i,knbe14)
= (sum((cell(i,j),w), fm_croparea("y1995",j,w,knbe14) * i14_yields_calib("y1995",j,knbe14,w)) /
sum((cell(i,j),w), fm_croparea("y1995",j,w,knbe14)))$(sum((cell(i,j),w), fm_croparea("y1995",j,w,knbe14))>0)
+ (sum((cell(i,j),w), i14_croparea_total("y1995",w,j) * f14_yields("y1995",j,knbe14,w)) /
sum((cell(i,j),w), i14_croparea_total("y1995",w,j)))$(sum((cell(i,j),w), fm_croparea("y1995",j,w,knbe14))=0);
i14_yields_calib(t,j,knbe14,w) = sum((cell(i,j)), i14_fao_yields_hist("y1995",i,knbe14) /
i14_modeled_yields_hist2(i,knbe14)) *
i14_yields_calib(t,j,knbe14,w);
pm_yields_semi_calib(j,knbe14,w) = i14_yields_calib("y1995",j,knbe14,w);
);Calibrated yields are additionally adjusted by calibration factors ‘f14_yld_calib’ determined in a calibration run. As MAgPIE optimizes yield patterns and FAO regional yields are outlier corrected, historical production and croparea can only be reproduced with this additional step of correction:
if(sum((i,ltype14),f14_yld_calib(i,ltype14)) = 0,
f14_yld_calib(i,ltype14) = 1;
);
i14_yields_calib(t,j,kcr,w) = i14_yields_calib(t,j,kcr,w) *sum(cell(i,j),f14_yld_calib(i,"crop"));
i14_yields_calib(t,j,"pasture",w) = i14_yields_calib(t,j,"pasture",w)*sum(cell(i,j),f14_yld_calib(i,"past"));carbon density. We convert Carbon density in tC/ha to tDM/ha by using carbon fraction of s14_carbon_fraction in tC/tDM. For assessing wood harvesting we need only aboveground biomass information, therefore we multiply with aboveground f14_aboveground_fraction. Additionally, we divide aboveground tree biomass by biomass conversion and expansion (BCE) factor to get stem biomass in tDM/ha.
Limitations The exogenous implementation of pasture intensification cannot capture feedbacks between land scarcity and efforts to improve pasture management. Moreover, the magnitude of spillover effects from technological change in the crop sector towards improvements in pasture management is very uncertain.
| Description | Unit | A | |
|---|---|---|---|
| f14_aboveground_fraction (forest_land) |
Root to shoot ratio | \(1\) | x |
| f14_fao_yields_hist (t_all, i, kcr) |
FAO yields per region | \(tDM/ha/yr\) | x |
| f14_ipcc_bce (clcl, forest_type) |
IPCC Biomass Conversion and Expansion factors | \(1\) | x |
| f14_ir2rf_ratio (i) |
AQUASTAT ratio of irrigated to rainfed yields per region | \(1\) | x |
| f14_pyld_hist (t_all, i) |
Modelled regional pasture yields in the past | \(tDM/ha/yr\) | x |
| f14_yields (t_all, j, kve, w) |
LPJmL potential yields per cell (rainfed and irrigated) | \(tDM/ha/yr\) | x |
| f14_yld_calib (i, ltype14) |
Calibration factor for the LPJmL yields | \(1\) | x |
| i14_calib_yields_hist (i, w) |
Calibrated yields average over region and crop type at the historical reference year | \(tDM/ha/yr\) | x |
| i14_calib_yields_ratio (i) |
Irrigated to rainfed yield ratio for calibrated yields | \(1\) | x |
| i14_croparea_total (t_all, w, j) |
Cellular croparea | \(10^6 ha\) | x |
| i14_fao_yields_hist (t, i, kcr) |
FAO yields per region at the historical referende year | \(tDM/ha/yr\) | x |
| i14_lambda_yields (t, i, kcr) |
Scaling factor for non-linear management calibration | \(1\) | x |
| i14_managementcalib (t, j, kcr, w) |
Regional management calibration factor accounting for FAO yield levels | \(1\) | x |
| i14_modeled_yields_hist (t_all, i, kcr) |
Biophysical input yields average over region and water supply type at the historical reference year | \(tDM/ha/yr\) | x |
| i14_modeled_yields_hist2 (i, knbe14) |
Calibrated yields average over region and water supply type at the historical reference year | \(tDM/ha/yr\) | x |
| i14_target_ratio (i) |
Target irrigated to rainfed ratio as upper bound | \(1\) | x |
| i14_yields_calib (t, j, kve, w) |
Calibrated biophysical input yields (excluding technological change) | \(tDM/ha/yr\) | x |
| p14_growing_stock (t, j, ac, forest_land, forest_type) |
Forest growing stock | \(tDM/ha/yr\) | x |
| p14_growing_stock_initial (j, ac, forest_land, forest_type) |
Initial Forest growing stock | \(tDM/ha/yr\) | x |
| p14_pyield_corr (t, i) |
Regional pasture management correction for historical time steps | \(1\) | x |
| p14_pyield_LPJ_reg (t_all, i) |
Regional average input yields aggregated from clusters with initial pasture area as weights | \(tDM/ha/yr\) | x |
| q14_yield_crop (j, kcr, w) |
Crop yields | \(tDM/ha/yr\) | x |
| q14_yield_past (j, w) |
Pasture yields | \(tDM/ha/yr\) | x |
| s14_calib_ir2rf | Switch to calibrate rainfed to irrigated yield ratios | \(1=calib 0=not calib\) | x |
| s14_carbon_fraction | Carbon fraction for conversion of biomass to dry matter | \(1\) | x |
| s14_limit_calib | Relative managament calibration switch | \(1=limited 0=pure relative\) | x |
| s14_timber_plantation_yield | Plantation yield switch (0=natveg yields 1=plantation yields) | \(1\) | x |
| s14_yld_past_switch | Spillover parameter for translating technological change in the crop sector into pasture yield increases | \(1\) | x |
| description | |
|---|---|
| ac | Age classes |
| ag_pools(c_pools) | Above ground carbon pools |
| cell(i, j) | number of LPJ cells per region i |
| clcl | climate classification types |
| ct(t) | Current time period |
| forest_land(land) | land from which timber can be taken away |
| forest_type | forest type |
| h | all superregional economic regions |
| h2(h) | Superregional (dynamic set) |
| i | all economic regions |
| i2(i) | World regions (dynamic set) |
| j | number of LPJ cells |
| j2(j) | Spatial Clusters (dynamic set) |
| k(kall) | Primary products |
| kall | All products in the sectoral version |
| kcr(kve) | Cropping activities |
| knbe14(kcr) | Cropping activities excluding bioenergy plants |
| kve(k) | Land-use activities |
| land | Land pools |
| land_natveg(forest_land) | Natural vegetation land pools |
| ltype14 | calibration land types |
| supreg(h, i) | mapping of superregions to its regions |
| t_all(t_ext) | 5-year time periods |
| t_past(t_all) | Timesteps with observed data |
| t(t_all) | Simulated time periods |
| tautype | tc type |
| type | GAMS variable attribute used for the output |
| w | Water supply type |
Jan Philipp Dietrich, Isabelle Weindl, Florian Humpenöder, Anne Biewald, Kristine Karstens
09_drivers, 10_land, 13_tc, 17_production, 30_crop, 31_past, 32_forestry, 35_natveg, 45_climate, 52_carbon, 70_livestock
Bondeau, Alberte, Pascalle C. Smith, Sönke Zaehle And Sibyll Schaphoff, Wolfgang Lucht, Wolfgang Cramer, Dieter Gerten, Hermann Lotze-Campen, Christoph Müller, Markus Reichstein, and Benjamin Smith. 2007. “Modelling the Role of Agriculture for the 20th Century Global Terrestrial Carbon Balance.” Global Change Biology 13 (3): 679–706. https://doi.org/10.1111/j.1365-2486.2006.01305.x.
FAO. 2016. AQUASTAT Core Database. Rome: Food; Agriculture Organization of the United Nations (FAO).
FAOSTAT. 2016. “FAOSTAT Database.” Rome: The Food; Agriculture Organization of the United Nations (FAO). http://www.fao.org/faostat/en/.
Heinke, J., S. Ostberg, S. Schaphoff, K. Frieler, C. Müller, D. Gerten, M. Meinshausen, and W. Lucht. 2013. “A New Climate Dataset for Systematic Assessments of Climate Change Impacts as a Function of Global Warming.” Geoscientific Model Development 6 (5): 1689–1703. https://doi.org/10.5194/gmd-6-1689-2013.