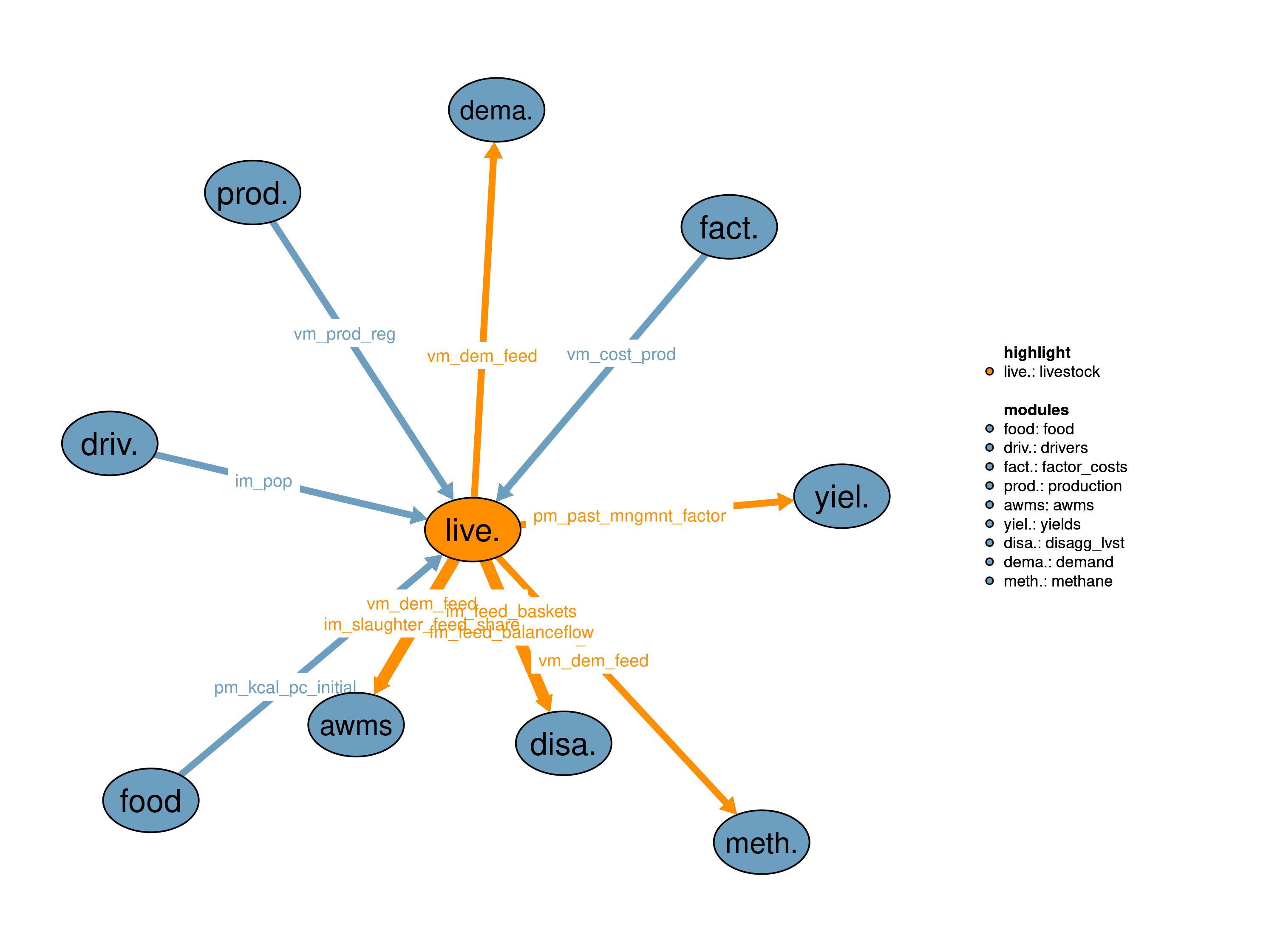
The livestock module calculates how much and what kind of biomass is required as feed to produce livestock food commodities.
For this purpose, the livestock module provides for every time-step regional and product-specific feed baskets that determine type and magnitude of feed needed to produce one unit of livestock commodities. Estimated pasture feed demand is also relevant for the module 31_past in order to derive required pasture areas. The information flow between the livestock and the pasture module is organized via interfaces vm_dem_feed, vm_supply and vm_prod_reg via modules 16_demand and 21_trade. Feed demand estimates are also required for the modules 53_methane and 55_awms. Additionally, the livestock module provides production costs for livestock commodities.
| Description | Unit | A | |
|---|---|---|---|
| im_pop (t, i) |
Population | \(10^6/yr\) | x |
| pm_kcal_pc_initial (t, i, kfo) |
Per capita consumption in food demand model before price shock | \(kcal/capita/day\) | x |
| vm_cost_prod (i, kall) |
Factor costs | \(10^6 USD_{05MER}/yr\) | x |
| vm_prod_reg (i, kall) |
Regional aggregated production | \(10^6 tDM/yr\) | x |
| Description | Unit | |
|---|---|---|
| fm_feed_balanceflow (t_all, i, kap, kall) |
Balanceflow balance difference between estimated feed baskets and FAO | \(10^6 tDM\) |
| im_feed_baskets (t_all, i, kap, kall) |
Feed baskets in tDM per tDM livestock product | \(1\) |
| im_slaughter_feed_share (t_all, i, kap, attributes) |
Share of feed that is incorporated in animal biomass | \(1\) |
| pm_past_mngmnt_factor (t, i) |
Regional pasture management intensification factor | \(1\) |
| vm_dem_feed (i, kap, kall) |
Regional feed demand including byproducts | \(10^6 tDM/yr\) |
The fbask_jan16 realization of the livestock module is based on the methodology as described in Weindl, Bodirsky, et al. (2017) and Weindl, Popp, et al. (2017). An important part of the feed demand calculations is conducted outside of the core MAgPIE-GAMS code. Livestock products (ruminant meat, whole-milk, pork, poultry meat and eggs) are supplied by five animal food systems (beef cattle, dairy cattle, pigs, broilers and laying hens). The parameterization of the livestock sector in the initial year is consistent with FAO statistics regarding livestock production, livestock productivity and concentrate feed use. The fbask_jan16 realization requires regional and product-specific feed baskets that are calculated by a set of preprocessing routines outside of the MAgPIE-GAMS code. Following the methodology of Wirsenius (2000), feed conversion (total feed input per product output in dry matter) and feed baskets (demand for different feed types per product output in dry matter) are derived by compiling system-specific feed energy balances. For the establishment of these balances, we apply feed energy requirements per output, as estimated by wirsenius_human_2000 for each animal function and animal food system. These estimates are based on standardized bio-energetic equations and include the minimum energy requirements for maintenance, growth, lactation, reproduction and other basic biological functions of the animals. Moreover, they comprise a general allowance for basic activity and temperature effects. By distributing the available feed at country level to animal food systems according to their feed energy demand and dividing resulting dry matter feed use by the production volume of the respective systems, we obtain both estimates for feed conversion and feed baskets across different animal food systems and countries. To facilitate projections of feed conversion and feed baskets, we create regression models with livestock productivity (annual production per animal [ton fresh matter/animal/year]) as predictor, which permit the construction of livestock feeding scenarios. Currently, feeding scenarios are derived based on exogenous livestock productivity scenarios consistent with the storylines of the Shared Socioeconomic Pathways (SSPs). For beef cattle, pigs and broilers, livestock productivity is defined as meat production per animals in stock (e.g. total cattle herd) and for dairy cattle and laying hen as milk or egg production per producing animals (e.g. milk cows). A power function is used to describe the functional relation between feed conversion and livestock productivity:  In the case of feed composition, we use an additional proxy parameter in our analysis. What type of biomass is used to feed animals is to a certain extent influenced by universal aspects (e.g. the need for more energy-rich feed at higher productivity levels), whereas other aspects are strongly influenced by geographical location (e.g. availability and costs of permanent pasture compared to cropland feed, agro-ecological and climatic conditions that favour selected feed items; socio-cultural determinants etc.). For cattle systems the proxy (climate-zone specific factor) was determined by calculating the share of the national population living in arid and cold climate zones.
In the case of feed composition, we use an additional proxy parameter in our analysis. What type of biomass is used to feed animals is to a certain extent influenced by universal aspects (e.g. the need for more energy-rich feed at higher productivity levels), whereas other aspects are strongly influenced by geographical location (e.g. availability and costs of permanent pasture compared to cropland feed, agro-ecological and climatic conditions that favour selected feed items; socio-cultural determinants etc.). For cattle systems the proxy (climate-zone specific factor) was determined by calculating the share of the national population living in arid and cold climate zones. 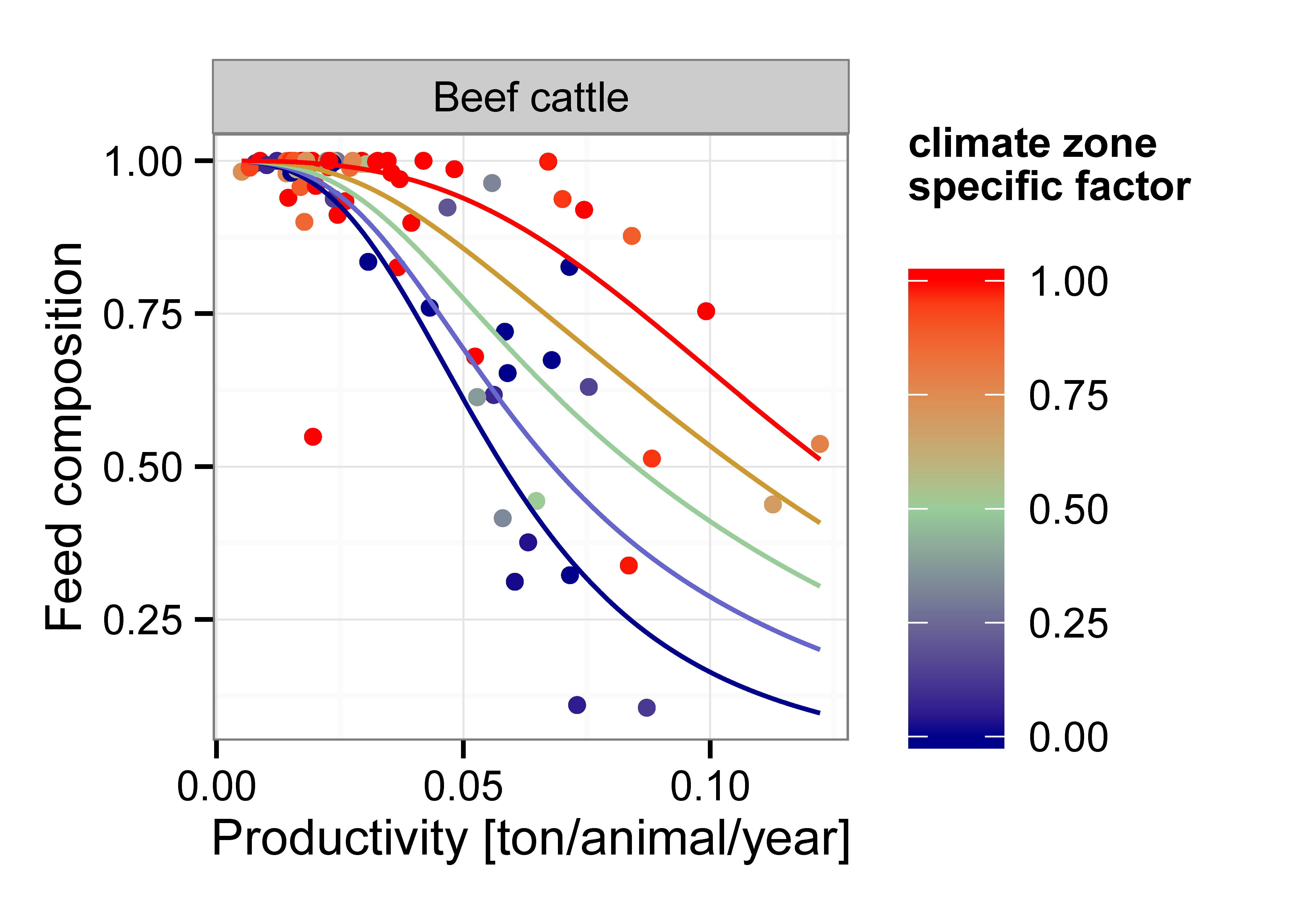
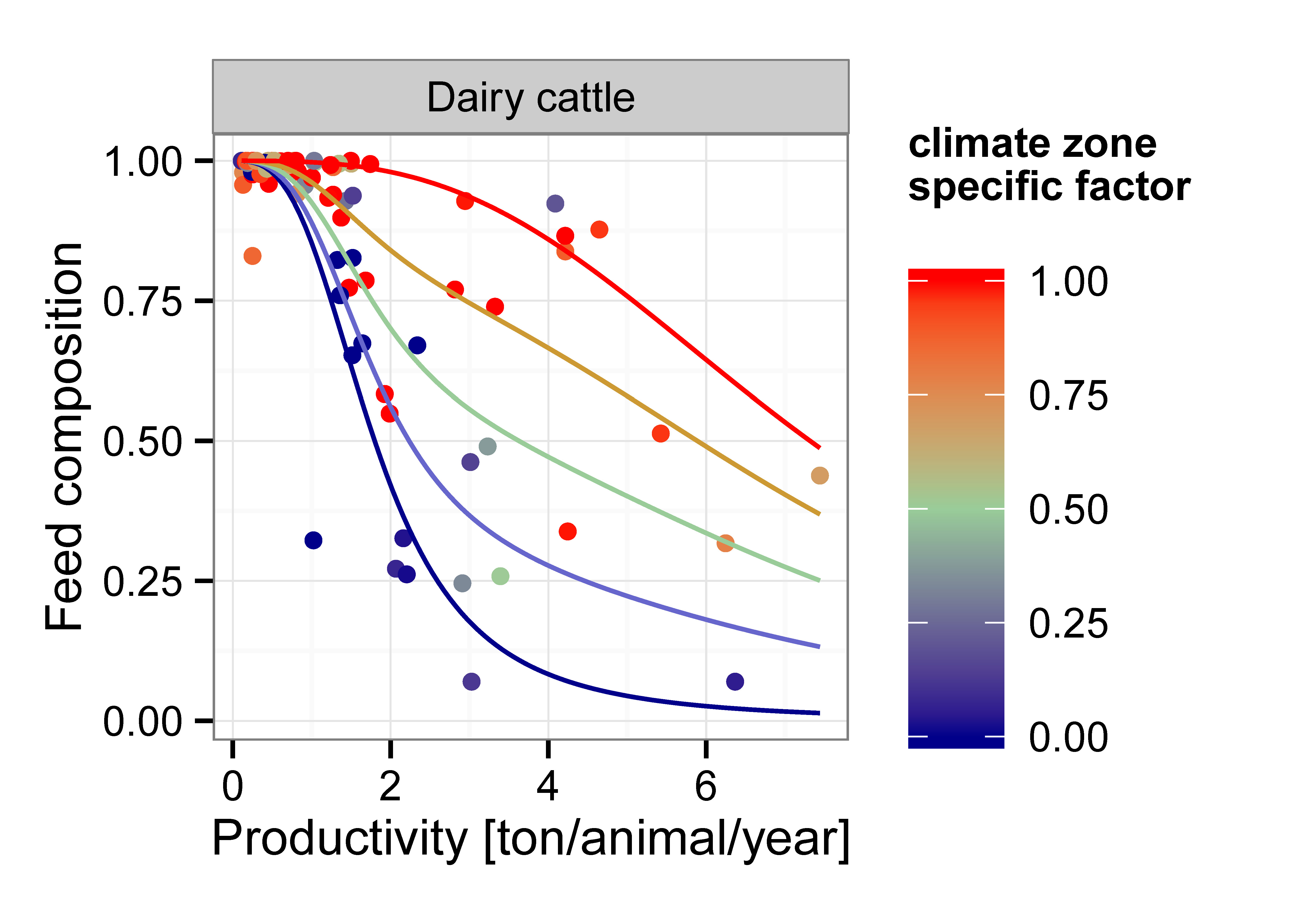 These relationships between feed baskets and livestock productivity are used to construct feeding scenarios that reflect the narratives of the SSPs. The resulting feed baskets enter the MAgPIE model as scenario-dependent input data and are crucial for the feed demand calculations in the livestock module.
These relationships between feed baskets and livestock productivity are used to construct feeding scenarios that reflect the narratives of the SSPs. The resulting feed baskets enter the MAgPIE model as scenario-dependent input data and are crucial for the feed demand calculations in the livestock module.
Demand for different feed items is derived by multiplying the regional livestock production with the respective feed baskets. Additionally, inconsistencies with the FAO inventory of national feed use in the case of crops as well as consideration of alternative feed sources that reduce e.g. the demand for grazed biomass like scavenging and roadside grazing are balanced out by the parameter fm_feed_balanceflow.
\[\begin{multline*} vm\_dem\_feed(i2,kap,kall) \geq vm\_prod\_reg(i2,kap) \cdot \sum_{ct}\left(f70\_feed\_baskets\left(ct,i2,kap,kall,"\%c70\_feed\_scen\%"\right)\right) +\sum_{ct}fm\_feed\_balanceflow(ct,i2,kap,kall) \end{multline*}\]
Factor requirement costs (e.g. labour, capital, but without costs for feed) of livestock production depend on the amount of production and the per-unit costs. For ruminant products (milk and meet), we use a regression of per-unit factor costs from the GTAP database (Narayanan and Walmsley 2008) and livestock productivity. Here, factor costs rise with intensification. The per-unit costs for non-ruminants and fish are assumed to be independent from productivity trajectories for simplification. Therefore, f70_cost_regr(kli,"cost_regr_b") is set to zero in the case of livestock products generated in monogastric systems.
\[\begin{multline*} vm\_cost\_prod(i2,kli) = vm\_prod\_reg(i2,kli) \cdot \left(f70\_cost\_regr(kli,"cost\_regr\_a") + f70\_cost\_regr(kli,"cost\_regr\_b") \cdot \sum_{ct, sys\_to\_kli(sys,kli)}\left(f70\_livestock\_productivity\left(ct,i2,sys,"\%c70\_feed\_scen\%"\right)\right)\right) \end{multline*}\]
\[\begin{multline*} vm\_cost\_prod(i2,"fish") = vm\_prod\_reg(i2,"fish") \cdot f70\_cost\_regr("fish","cost\_regr\_a") \end{multline*}\]
The fbask_jan16 realization of the livestock module also estimates an exogenous pasture management factor pm_past_mngmnt_factor that is used to scale biophysical pasture yields in the module 14_yields. The exogenous calculation of pasture management requires information on the number of cattle reared to fulfil the domestic demand for ruminant livestock products:
p70_cattle_stock_proxy(t,i) = im_pop(t,i)*pm_kcal_pc_initial(t,i,"livst_rum")
/i70_livestock_productivity(t,i,"sys_beef"); The lower bound for p70_cattle_stock_proxy is set to 20% of initial cattle stocks in 1995:
p70_cattle_stock_proxy(t,i)$(p70_cattle_stock_proxy(t,i) < 0.2*p70_cattle_stock_proxy("y1995",i)) = 0.2*p70_cattle_stock_proxy("y1995",i);The parameter p70_incr_cattle describes the changes in cattle stocks relative to the previous time step:
p70_incr_cattle(t,i) = 1$(ord(t)=1)
+ (p70_cattle_stock_proxy(t,i)/p70_cattle_stock_proxy(t-1,i))$(ord(t)>1);The pasture management factor is calculated by applying a linear relationship that links changes in pasture management with changes in cattle stocks:
if (sum(sameas(t_past,t),1) = 1,
pm_past_mngmnt_factor(t,i) = 1;
else
pm_past_mngmnt_factor(t,i) = ( (s70_pyld_intercept + f70_pyld_slope_reg(i)*p70_incr_cattle(t,i)**(5/(m_year(t)-m_year(t-1)))
)**((m_year(t)-m_year(t-1))/5) )*pm_past_mngmnt_factor(t-1,i);
);Limitations Intensification of livestock production and related changes in livestock feeding are modelled exogenously. Therefore, the livestock sector does not endogenously respond to demand and climate shocks and policies, e.g. targeting climate protection.
| Description | Unit | A | |
|---|---|---|---|
| f70_cost_regr (kap, cost_regr) |
Factor requirements livestock (USD04 per tDM (A) and USD | \(B)\) | x |
| f70_feed_baskets (t_all, i, kap, kall, feed_scen70) |
Feed baskets in tDM per tDM livestock product | \(1\) | x |
| f70_livestock_productivity (t_all, i, sys, feed_scen70) |
Productivity indicator for livestock production | \(t FM/animal\) | x |
| f70_pyld_slope_reg (i) |
Regional slope of linear relationship determining pasture intensification | \(1\) | x |
| f70_slaughter_feed_share (t_all, i, kap, attributes, feed_scen70) |
Share of feed that is incorprated in animal biomass | \(1\) | x |
| i70_livestock_productivity (t_all, i, sys) |
Productivity indicator for livestock production | \(t FM/animal/yr\) | x |
| p70_cattle_stock_proxy (t, i) |
Proxy for cattle stocks needed to fullfil domestic food demand | \(10^6 animals/yr\) | x |
| p70_incr_cattle (t, i) |
Change in estimated cattle stocks attributed to food demand projections | \(1\) | x |
| q70_cost_prod_fish (i) |
Regional factor input costs for fish production | x | |
| q70_cost_prod_liv (i, kall) |
Regional factor input costs for livestock production | x | |
| q70_feed (i, kap, kall) |
Regional feed demand | x | |
| s70_pyld_intercept | Intercept of linear relationship determining pasture intensification | \(1\) | x |
| description | |
|---|---|
| attributes | Product attributes characterizing a product (such as weight or energy content) |
| cost_regr | Cost regression parameters |
| ct(t) | Current time period |
| feed_scen70 | scenarios |
| i | World regions |
| i2(i) | World regions (dynamic set) |
| kall | All products in the sectoral version |
| kap(k) | Animal products |
| kfo(kall) | All products in the sectoral version |
| kli(kap) | Livestock products |
| sys | Livestock production systems |
| sys_meat(sys) | Livestock meat production systems |
| sys_nonmeat(sys) | Livestock non-meat production systems |
| sys_to_kli(sys, kli) | Mapping between livestock producton systems and livestock products |
| t_all | 5-year time periods |
| t_past(t_all) | Timesteps with observed data |
| t(t_all) | Simulated time periods |
| type | GAMS variable attribute used for the output |
Isabelle Weindl, Benjamin Bodirsky
09_drivers, 14_yields, 15_food, 16_demand, 17_production, 38_factor_costs, 53_methane, 55_awms, 71_disagg_lvst
Narayanan, G. Badri, and Eds. Walmsley Terrie L. 2008. Global Trade, Assistance, and Production: The Gtap 7 Data Base. Center for Global Trade Analysis, Purdue University. http://www.gtap.agecon.purdue.edu/databases/v7/v7_doco.asp.
Weindl, Isabelle, Benjamin Leon Bodirsky, Susanne Rolinski, Anne Biewald, Hermann Lotze-Campen, Christoph Müller, Jan Philipp Dietrich, et al. 2017. “Livestock Production and the Water Challenge of Future Food Supply: Implications of Agricultural Management and Dietary Choices.” Global Environmental Change 47 (Supplement C): 121–32. https://doi.org/10.1016/j.gloenvcha.2017.09.010.
Weindl, Isabelle, Alexander Popp, Benjamin Leon Bodirsky, Susanne Rolinski, Hermann Lotze-Campen, Anne Biewald, Florian Humpenöder, Jan Philipp Dietrich, and Miodrag Stevanovic. 2017. “Livestock and Human Use of Land: Productivity Trends and Dietary Choices as Drivers of Future Land and Carbon Dynamics.” Global and Planetary Change 159 (Supplement C): 1–10. https://doi.org/10.1016/j.gloplacha.2017.10.002.
Wirsenius, Stefan. 2000. “Human Use of Land and Organic Materials: Modeling the Turnover of Biomass in the Global Food System.” Doctoral thesis, Chalmers University of Technology. http://publications.lib.chalmers.se/publication/827-human-use-of-land-and-organic-materials-modeling-the-turnover-of-biomass-in-the-global-food-system.