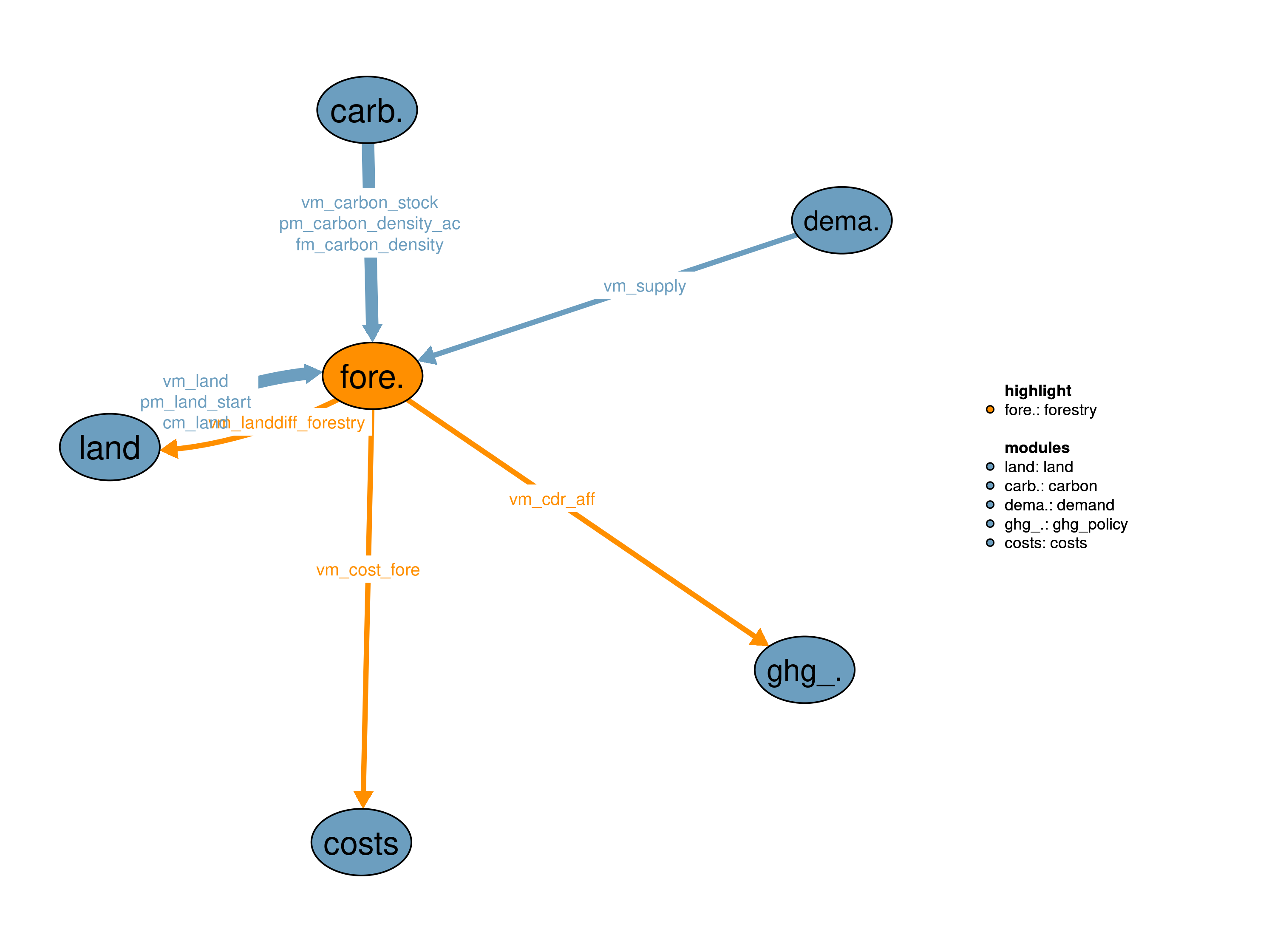
The forestry module describes the constraints under which managed forest (age-class forest) exists. At the same time it calculates the corresponding carbon stocks. The module provides carbon dioxide removal (CDR) from afforestation to the GHG policy module (56_ghg_policy) as well as afforestation related costs to the costs module (11_costs).
| Description | Unit | A | B | |
|---|---|---|---|---|
| fm_carbon_density (t_all, j, land, c_pools) |
LPJmL carbon density for land and carbon pools | \(tC/ha\) | x | x |
| pcm_land (j, land) |
Land area in previous time step | \(10^6 ha\) | x | x |
| pm_carbon_density_ac (t, j, ac, c_pools) |
Carbon density for age classes and carbon pools | \(tC/ha\) | x | |
| pm_land_start (j, land) |
Land initialization area | \(10^6 ha\) | x | |
| vm_carbon_stock (j, land, c_pools) |
Carbon stock in vegetation soil and litter for different land types | \(10^6 tC\) | x | x |
| vm_land (j, land) |
Land area of the different land types | \(10^6 ha\) | x | x |
| vm_supply (i, kall) |
Regional demand | \(10^6 tDM/yr\) | x | x |
| Description | Unit | |
|---|---|---|
| vm_cdr_aff (j) |
Total CDR from afforestation (new and existing areas) between t+1 and t=s32_planing_horizon CO2-C | \(10^6 tC\) |
| vm_cost_fore (i) |
Afforestation costs | \(10^6 USD_{04MER}/yr\) |
| vm_landdiff_forestry | Aggregated difference in forestry land compared to previous timestep | \(10^6 ha\) |
The main feature of the affore_vegc_dec16 realization is afforestation for CDR. Afforestation can be modelled exogenously (prescribed by NPI/NDC policies) and/or endogenously (incentivized by a reward for CDR). National policies implemented (NPI) and nationally determined contributions to the Paris agreement (NDC) for afforestation are based on country reports. The reward for CDR from afforestation vm_cdr_aff consists of the projected CDR within a planing horizon of 30 years s32_planing_horizon multiplied with the carbon price and annuity factor in the 56_ghg_policy module. Technically, the reward for CDR from afforestation is a negative cash flow lowering the costs in the objective function of the model. In this realization, afforestation is modeled as managed/assisted regrowth of natural vegetation (Humpenöder et al. (2014)). The regrowth of natural vegetation follows S-shaped growth curves. Note that existing forestry plantations in 1995 dedicated to wood production are assumed constant throughout time.
The direct costs of afforestation vm_cost_fore include maintenance and monitoring costs for newly established plantations (Sathaye et al. 2005). Note that “old” refers to forestry plantations for wood production in 1995. In addition, afforestation may cause costs in other parts of the model such as costs for technological change 13_tc or land expansion 39_landconversion.
\[\begin{multline*} vm\_cost\_fore(i2) = \sum_{\left(cell(i2,j2),land32,fcosts32\right)\$\left(not sameas(land32,"old")\right)}\left( v32\_land(j2,land32) \cdot f32\_fac\_req\_ha(i2,fcosts32)\right) \end{multline*}\]
The interface vm_cdr_aff provides the projected CDR of an afforestation activity for a planning horizon of 30 years s32_planing_horizon to the 56_ghg_policy module.
\[\begin{multline*} vm\_cdr\_aff(j2) = \sum_{ac\$\left(ord(ac) > 1 \& \left(ord(ac)-1\right) \leq\frac{ s32\_planing\_horizon}{5}\right)}\left( v32\_land(j2,"new") \cdot \left(\sum_{ct} pm\_carbon\_density\_ac(ct,j2,ac,"vegc") - \sum_{ct} pm\_carbon\_density\_ac(ct,j2,ac-1,"vegc")\right)\right) \end{multline*}\]
The interface vm_land provides aggregated forestry land pools (land32) to other modules.
\[\begin{multline*} vm\_land(j2,"forestry") = \sum_{land32} v32\_land(j2,land32) \end{multline*}\]
The constraint q32_aff_pol accounts for the exogenous afforestation prescribed by NPI/NDC policies.
\[\begin{multline*} v32\_land(j2,"new\_ndc") = \sum_{ct} p32\_aff\_pol\_timestep(ct,j2) \end{multline*}\]
The constraint q32_max_aff accounts for the allowed maximum global endogenous afforestation defined in s32_max_aff_area. Note that NPI/NDC afforestation policies are not counted towards the maximum defined in s32_max_aff_area. Therefore, the constraint is relaxed by the value of exogenously prescribed afforestation (p32_aff_togo).
\[\begin{multline*} \sum_{j2}\left( vm\_land(j2,"forestry")-pm\_land\_start(j2,"forestry")\right) \leq s32\_max\_aff\_area - \sum_{ct} p32\_aff\_togo(ct) \end{multline*}\]
Forestry carbon stocks are calculated as the product of forestry land (v32_land) and the area weighted mean of carbon density for carbon pools (p32_carbon_density).
\[\begin{multline*} vm\_carbon\_stock(j2,"forestry",c\_pools) = \sum_{land32}\left( v32\_land(j2,land32) \cdot \sum\left(ct, p32\_carbon\_density(ct,j2,land32,c\_pools)\right)\right) \end{multline*}\]
Forestry land expansion and reduction is calculated as follows:
\[\begin{multline*} vm\_landdiff\_forestry = \sum_{j2,land32}\left( v32\_land\_expansion(j2,land32) + v32\_land\_reduction(j2,land32)\right) \end{multline*}\]
\[\begin{multline*} v32\_land\_expansion(j2,land32) \geq v32\_land(j2,land32) - pc32\_land(j2,land32) \end{multline*}\]
\[\begin{multline*} v32\_land\_reduction(j2,land32) \geq pc32\_land(j2,land32) - v32\_land(j2,land32) \end{multline*}\]
Wood demand is set to zero because forestry is not modeled in this realization.
vm_supply.fx(i2,kforestry) = 0;Certain areas (e.g. the boreal zone) are excluded from endogenous afforestation.
v32_land.lo(j,"new") = 0;
v32_land.up(j,"new") = f32_aff_mask(j) * sum(land, pcm_land(j,land));Endogenous afforestation is limited to cells with vegetation carbon density above 20 tC/ha.
v32_land.fx(j,"new")$(fm_carbon_density(t,j,"forestry","vegc") <= 20) = 0;Limitations Forestry activities such as establishment or harvest of plantations for wood production are not modeled.
The static realisation is very simple and does not include any equation because forestry land is assumed constant at the observed 1995 level throughout time.
Costs and CDR from afforestation are set to zero.
vm_cost_fore.fx(i) = 0;
vm_cdr_aff.fx(j) = 0;All forestry land pools (land32) except for “old” are set to zero, whereas “old” refers to the forestry plantations at the level of 1995.
v32_land.fx(j,"new") = 0;
v32_land.fx(j,"prot") = 0;
v32_land.fx(j,"grow") = 0;
v32_land.fx(j,"old") = pcm_land(j,"forestry");Forestry carbon stocks are calculated by multiplying plantations in 1995 with the forestry carbon density of the current time step (pc32_carbon_density).
pc32_carbon_density(j,c_pools) = fm_carbon_density(t,j,"forestry",c_pools);
vm_carbon_stock.fx(j,"forestry",c_pools) = vm_land.l(j,"forestry")*pc32_carbon_density(j,c_pools);Wood demand is also set to zero because forestry is not modeled in this realization.
vm_supply.fx(i2,kforestry) = 0;Limitations Forestry activities such as establishment or harvest of plantations for wood production are not modeled. Also afforestation for CDR is not included.
| Description | Unit | A | B | |
|---|---|---|---|---|
| f32_aff_mask (j) |
Afforestation mask | \(1\) | x | |
| f32_aff_pol (t_all, j, pol32) |
Exogenous afforestation scenario | \(10^6 ha\) | x | |
| f32_fac_req_ha (i, fcosts32) |
Afforestation factor requirement costs per ha | \(USD_{04MER}/ha\) | x | |
| p32_aff_pol (t, j) |
Exogenous afforestation target as stock | \(10^6 ha\) | x | |
| p32_aff_pol_timestep (t, j) |
Exogenous afforestation target as flow per time step | \(10^6 ha/timestep\) | x | |
| p32_aff_pot (t, j) |
Potential afforestation area on cropland and pasture land | \(10^6 ha\) | x | |
| p32_aff_togo (t) |
Remaining exogenous afforestation wrt to the maximum exogenous target over time | \(10^6 ha\) | x | |
| p32_carbon_density (t, j, land32, c_pools) |
Carbon density for land32 and c_pools | \(tC/ha\) | x | |
| p32_land (t, j, ac, when) |
Forestry land for each cell wood type and age class before and after optimization | \(10^6 ha\) | x | |
| pc32_carbon_density (j, c_pools) |
Carbon density in optimization | \(tC/ha\) | x | |
| pc32_land (j, land32) |
Forestry land per forestry land type initialization of the optimization | \(10^6 ha\) | x | |
| q32_aff_pol (j) |
Afforestation policy constraint | \(10^6 ha\) | x | |
| q32_carbon (j, c_pools) |
Forestry carbon stock calculation C | \(10^6 tC\) | x | |
| q32_cdr_aff (j) |
Calculation of CDR from afforestation in terms of CO2-C | \(10^6 tC\) | x | |
| q32_cost_fore_ac (i) |
Total forestry costs constraint | \(10^6 USD_{04MER}\) | x | |
| q32_land (j) |
Land constraint | \(10^6 ha\) | x | |
| q32_land_diff | Aggregated difference in forestry land compared to previous timestep | \(10^6 ha\) | x | |
| q32_land_expansion (j, land32) |
Forestry land expansion | \(10^6 ha\) | x | |
| q32_land_reduction (j, land32) |
Forestry land reduction | \(10^6 ha\) | x | |
| q32_max_aff | Maximum total global afforestation | \(10^6 ha\) | x | |
| s32_max_aff_area | Maximum global endogenous afforestation | \(10^6 ha\) | x | |
| s32_planing_horizon | Afforestation planing horizon | \(years\) | x | x |
| s32_shift | Number of 5-year age-classes corresponding to current time step length | \(1\) | x | |
| v32_land (j, land32) |
Forestry land pools | \(10^6 ha\) | x | x |
| v32_land_expansion (j, land32) |
Forestry land expansion compared to previous timestep | \(10^6 ha\) | x | |
| v32_land_reduction (j, land32) |
Forestry land reduction compared to previous timestep | \(10^6 ha\) | x |
| description | |
|---|---|
| ac | Age classes |
| ac_land32(ac, land32) | Mapping between age class and forestry land type |
| age | Population age groups |
| c_pools | Carbon pools |
| cell(i, j) | Mapping between regions i and clusters j |
| ct(t) | Current time period |
| fcosts32 | Forestry factor cost types |
| i | World regions |
| i2(i) | World regions (dynamic set) |
| j | Spatial clusters |
| j2(j) | Spatial Clusters (dynamic set) |
| kall | All products in the sectoral version |
| kforestry(kall) | Forestry products |
| land | Land pools |
| land32 | Forestry land pools |
| pol32 | Afforestation policy |
| t_all | 5-year time periods |
| t(t_all) | Simulated time periods |
| type | GAMS variable attribute used for the output |
| when | Temporal location relative to optimization |
Florian Humpenöder
10_land, 11_costs, 16_demand, 52_carbon, 56_ghg_policy
Humpenöder, Florian, Alexander Popp, Jan Philip Dietrich, David Klein, Hermann Lotze-Campen, Markus Bonsch, Benjamin Leon Bodirsky, Isabelle Weindl, Miodrag Stevanovic, and Christoph Müller. 2014. “Investigating Afforestation and Bioenergy CCS as Climate Change Mitigation Strategies.” Environmental Research Letters 9 (6): 064029. https://doi.org/10.1088/1748-9326/9/6/064029.
Sathaye, Jayant, Willy Makundi, Larry Dale, Peter Chan, and Kenneth Andrasko. 2005. “GHG Mitigation Potential, Costs and Benefits in Global Forests: A Dynamic Partial Equilibrium Approach.” Lawrence Berkeley National Laboratory, March. http://escholarship.org/uc/item/92d5m16v.