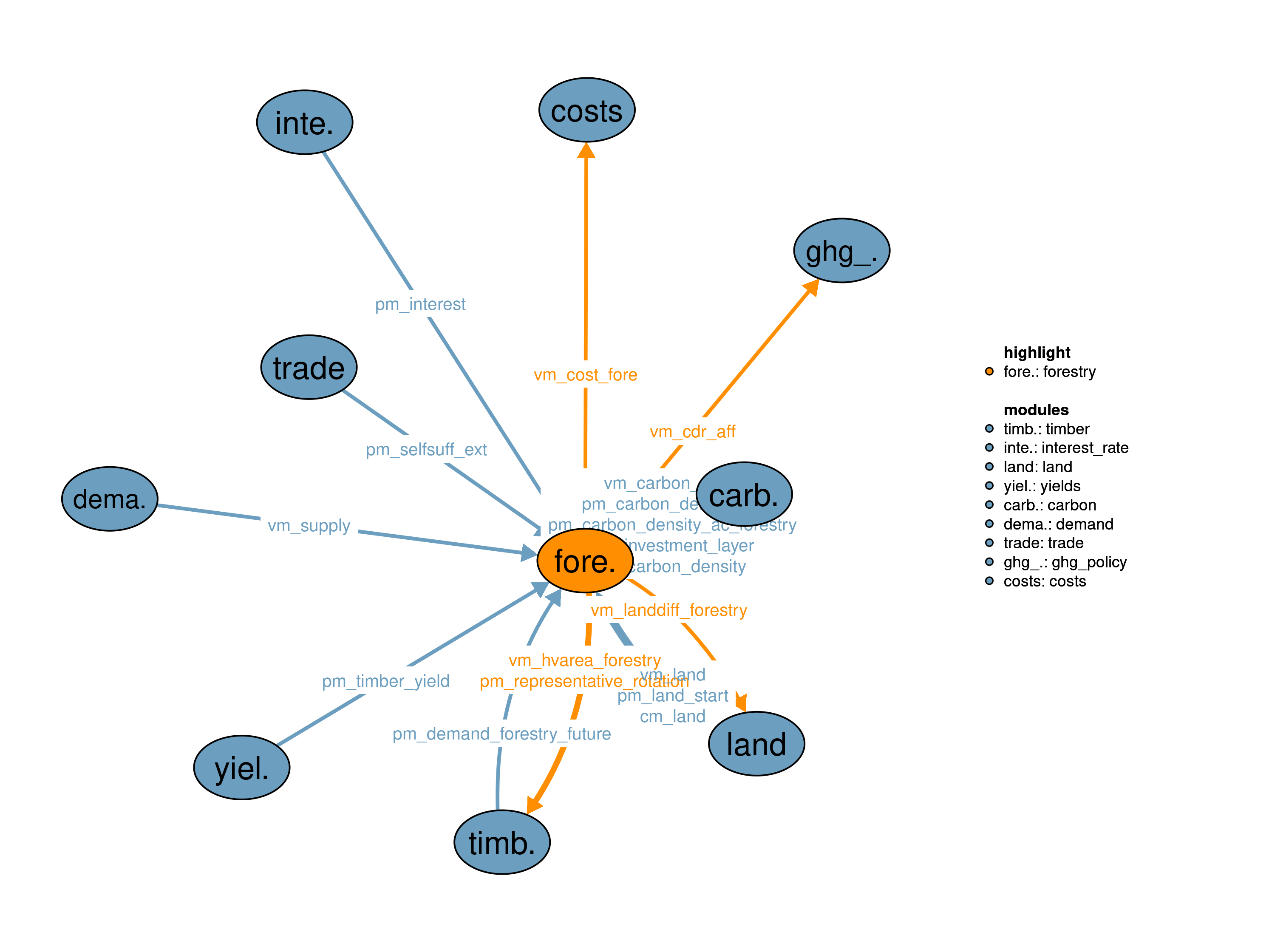
The forestry module describes the constraints under which managed forest (age-class forest) exists. At the same time it calculates the corresponding carbon stocks. The module provides carbon dioxide removal (CDR) from afforestation to the GHG policy module (56_ghg_policy) as well as afforestation related costs to the costs module (11_costs).
| Description | Unit | A | B | |
|---|---|---|---|---|
| fm_carbon_density (t_all, j, land, c_pools) |
LPJmL carbon density for land and carbon pools | \(tC/ha\) | x | x |
| pcm_land (j, land) |
Land area in previous time step | \(10^6 ha\) | x | x |
| pm_carbon_density_ac (t, j, ac, ag_pools) |
Above ground natveg carbon density for age classes and carbon pools | \(tC/ha\) | x | x |
| pm_carbon_density_ac_forestry (t_all, j, ac, ag_pools) |
Above ground plantation carbon density for age classes and carbon pools | \(tC/ha\) | x | |
| pm_demand_forestry_future (i, kforestry) |
Future forestry demand in current time step | \(tDM/yr\) | x | |
| pm_interest (t_all, i) |
Interest rate in each region and timestep | \(\%/yr\) | x | |
| pm_investment_layer (t_all, j) |
Difference between needed and observed LPJmL carbon densities in clusters where LPJmL values area lower than a threshold | \(tC/ha\) | x | |
| pm_land_start (j, land) |
Land initialization area | \(10^6 ha\) | x | |
| pm_selfsuff_ext (t_ext, i, kforestry) |
Self sufficiency for timber products in extended time frame | \(1\) | x | |
| pm_timber_yield (t, j, ac, forest_land) |
Forest growing stock | \(m3/ha/yr\) | x | |
| sm_fix_SSP2 | year until which all parameters are fixed to SSP2 values | \(year\) | x | |
| vm_carbon_stock (j, land, c_pools) |
Carbon stock in vegetation soil and litter for different land types | \(10^6 tC\) | x | x |
| vm_land (j, land) |
Land area of the different land types | \(10^6 ha\) | x | x |
| vm_supply (i, kall) |
Regional demand | \(10^6 tDM/yr\) | x |
| Description | Unit | |
|---|---|---|
| pm_representative_rotation (t_all, i) |
Representative regional rotation | \(1\) |
| vm_cdr_aff (j, ac, aff_effect) |
Expected bgc (CDR) and local bph effects of afforestation depending on planning horizon | \(10^6 tC\) |
| vm_cost_fore (i) |
Forestry costs | \(10^6 USD\) |
| vm_hvarea_forestry (j, ac) |
Harvested area from timber plantations | \(10^6 ha\) |
| vm_landdiff_forestry | Aggregated difference in forestry land compared to previous timestep | \(10^6 ha\) |
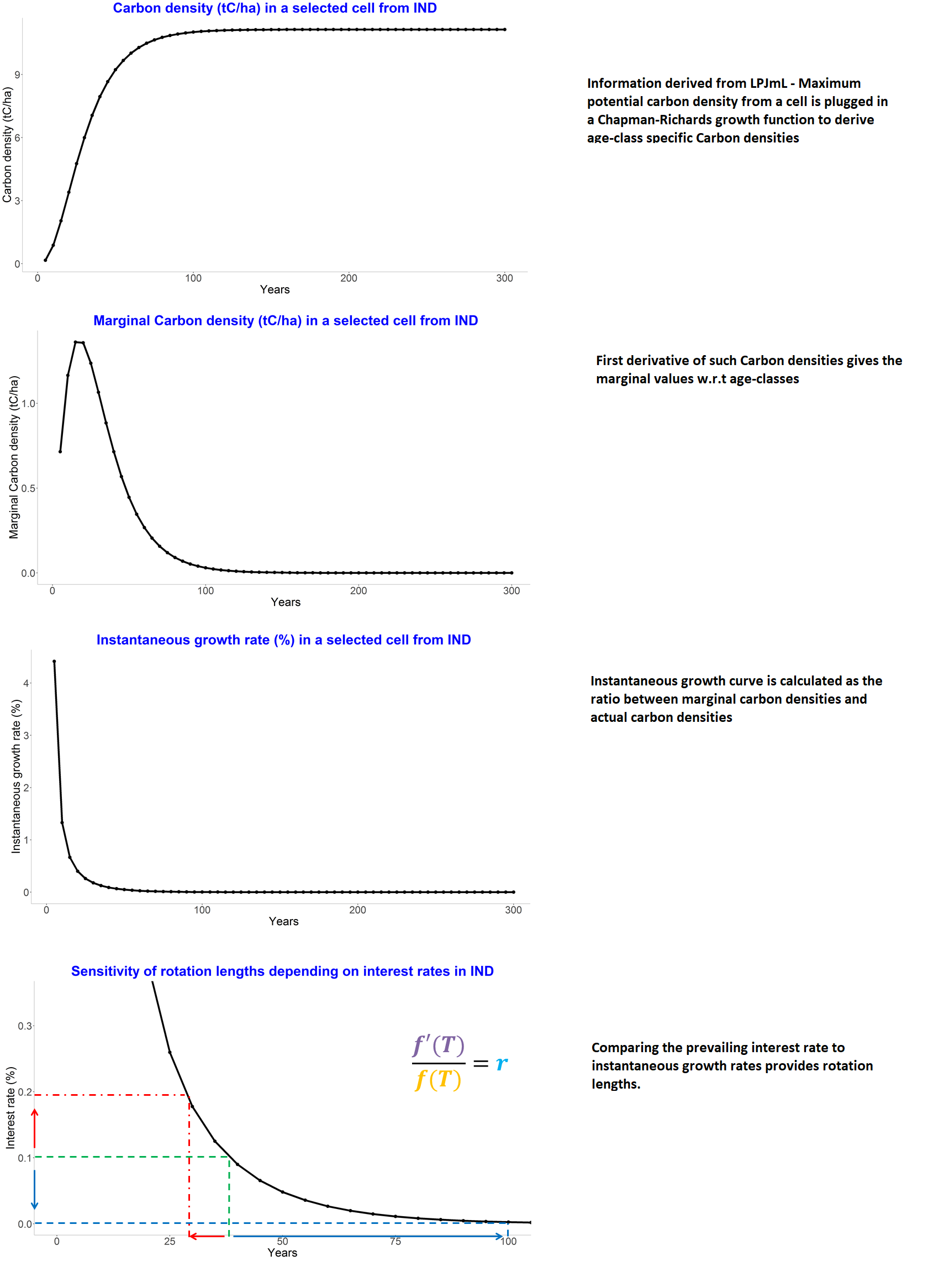
The main feature of the this realization is afforestation for CDR and timber production. Afforestation can be modelled exogenously (prescribed by NPI/NDC policies) and/or endogenously (incentivized by a reward for CDR). National policies implemented (NPI) and nationally determined contributions to the Paris agreement (NDC) for afforestation are based on country reports. The interface vm_cdr_aff includes the expected CDR and local bph effects from afforestation depending on the planning horizon s32_planing_horizon. The reward for CDR and local bph effects from afforestation is calculated in the 56_ghg_policy module. In this realization, afforestation is modeled by default as regrowth of natural vegetation (see Humpenöder et al. (2014) for details on the implemenation). The regrowth of natural vegetation follows S-shaped growth curves, which are parametrized based on Braakhekke et al. (2019). Additionally this module handles the production of two timber products i.e., wood and woodfuel from plantation forests while still accounting for afforestation policies. New plantations are also established in the simulation step to account for future timber demand. This module also calculates the rotation lengths before the solve loop by equating Instantaneous Growth Rates (IGR) and interest rate pm_interest based on Amacher, Ollikainen, and Koskela (2009). We have to make assumptions regarding the rotation lengths to be used for establishment and harvesting decisions. For establishment we just use the calculated rotations either based on a Single Rotation-Period Model or based on Faustamnn rotations according to the switch s32_faustmann_rotation. For harvesting we assume that land owners stick to their establishment decision, e.g. if a plantation has been established with a rotation length of 30 years it will be harvested after 30 years, even so the rotation length in the prevailing time step, used for establishment, is shorter or longer.
The direct costs of Timber production and afforestation vm_cost_fore include maintenance and monitoring costs for newly established plantations as well as standing plantations ’(Sathaye et al. 2005). In addition, this type of forest management (including afforestation) may cause costs in other parts of the model such as costs for technological change 13_tc or land expansion 39_landconversion. Also included are additional costs for producing timber from extremely highly managed plantations which are analogous to intensification using technological change from 13_tc but in a parametrized form.
\[\begin{multline*} vm\_cost\_fore(i2) = v32\_cost\_recur(i2) + v32\_cost\_establishment(i2) + \sum_{cell(i2,j2)} v32\_land\_missing(j2) \cdot s32\_free\_land\_cost + \sum_{cell(i2,j2)} v32\_cost\_extra\_investment(j2) \end{multline*}\]
The interface vm_cdr_aff provides the projected bgc (CDR) and local bph effects of an afforestation activity for a planning horizon of 30 years s32_planing_horizon to the 56_ghg_policy module.
\[\begin{multline*} vm\_cdr\_aff(j2,ac,"bgc") = \sum_{ac\_est} v32\_land(j2,"aff",ac\_est) \cdot \sum_{ct} p32\_cdr\_ac(ct,j2,ac) + \sum_{ac\_est} v32\_land(j2,"plant",ac\_est) \cdot \sum_{ct} p32\_cdr\_ac\_plant(ct,j2,ac) \end{multline*}\]
\[\begin{multline*} vm\_cdr\_aff(j2,ac,"bph") = v32\_land(j2,"aff","ac0") \cdot p32\_aff\_bgp(j2,ac) \end{multline*}\]
ac_est can only increase if total afforested land increases
\[\begin{multline*} \sum_{ac\_est} v32\_land(j2,"aff",ac\_est) \leq \sum_{ac} v32\_land(j2,"aff",ac) - \sum_{ct,ac} p32\_land(ct,j2,"aff",ac) \end{multline*}\]
The interface vm_land provides aggregated forestry land pools (type32) to other modules.
\[\begin{multline*} vm\_land(j2,"forestry") = \sum_{type32,ac} v32\_land(j2,type32,ac) \end{multline*}\]
The constraint q32_aff_pol accounts for the exogenous afforestation prescribed by NPI/NDC policies.
\[\begin{multline*} \sum_{ac\_est} v32\_land(j2,"ndc",ac\_est) = \sum_{ct} p32\_aff\_pol\_timestep(ct,j2) \end{multline*}\]
The constraint q32_max_aff accounts for the allowed maximum global afforestation defined in p32_max_aff_area. Note that NPI/NDC afforestation policies are counted towards the maximum defined in p32_max_aff_area. Therefore, the right-hand side of the constraint is tightened by the value of the exogenously prescribed afforestation that has to be realized in later time steps (p32_aff_togo).
\[\begin{multline*} \sum_{\left(j2,type32,ac\right)\$\left(not sameas(type32,"plant")\right)} v32\_land(j2,type32,ac) \leq p32\_max\_aff\_area - \sum_{ct} p32\_aff\_togo(ct) \end{multline*}\]
Forestry above ground carbon stocks are calculated as the product of forestry land (v32_land) and the area weighted mean of carbon density for carbon pools (p32_carbon_density_ac).
\[\begin{multline*} vm\_carbon\_stock(j2,"forestry",ag\_pools) = \sum_{type32,ac}\left( v32\_land(j2,type32,ac) \cdot \sum_{ct} p32\_carbon\_density\_ac(ct,j2,type32,ac,ag\_pools)\right) \end{multline*}\]
Forestry land expansion and reduction is calculated as follows:
\[\begin{multline*} vm\_landdiff\_forestry = \sum_{j2,type32,ac}\left( v32\_land\_expansion(j2,type32,ac) + v32\_land\_reduction(j2,type32,ac)\right) \end{multline*}\]
\[\begin{multline*} v32\_land\_expansion(j2,type32,ac\_est) = v32\_land(j2,type32,ac\_est) - pc32\_land(j2,type32,ac\_est) \end{multline*}\]
\[\begin{multline*} v32\_land\_reduction(j2,type32,ac\_sub) = pc32\_land(j2,type32,ac\_sub) - v32\_land(j2,type32,ac\_sub) \end{multline*}\]
Cost of new plantations establishment v32_cost_establishment is the investment made in setting up new plantations but also accounts for the expected value of future harvesting costs. This makes sure that the model sticks to reasonable plantation patterns over time. Present value of harvesting costs is (1+pm_interest)^p32_rotation_regional and annuity factor of pm_interest/(1+pm_interest) averages the cost of this investment over time.
\[\begin{multline*} v32\_cost\_establishment(i2) = \left(\sum_{cell(i2,j2),type32}\left( v32\_land(j2,type32,"ac0") \cdot s32\_reESTBcost\right) \right) \cdot \sum_{ct}\left(\frac{pm\_interest(ct,i2)}{\left(1+pm\_interest(ct,i2)\right)}\right) \end{multline*}\]
Recurring costs are paid for plantations where the trees have to be regularly monitored and maintained. These costs are only calculated becuase we see active human intervention in commercial plantations. These costs are paid for trees used for timber production or trees established for afforestation purposes.
\[\begin{multline*} v32\_cost\_recur(i2) = \sum_{cell(i2,j2),type32,ac\_sub} v32\_land(j2,type32,ac\_sub) \cdot s32\_recurring\_cost \end{multline*}\]
New plantations are already established in the optimization step based on a certain percentage (pc32_plant_prod_share_future) of future demand (pm_demand_forestry_future) This is based on the expected future yield (pc32_yield_forestry_future) at harvest (year in time step are accounted for). Here we define three constraints for establishing new plantation in simulation step Fix plantation area at cell level if s32_fix_plant=1. In case of s32_fix_plant=0, the RHS is just 0. This makes sure that if plantation area is constrained when the switch is activated.
\[\begin{multline*} \sum_{ac} v32\_land(j2,"plant",ac) \geq \sum_{ct,ac} p32\_land(ct,j2,"plant",ac) \cdot \sum_{ct}p32\_fix\_plant(ct) \end{multline*}\]
Global maximum constraint based on meeting all the future timber demand (pm_demand_forestry_future).
\[\begin{multline*} \sum_{j2}\left(\frac{ \left(\sum\left(ac\_est, v32\_land(j2,"plant",ac\_est)\right) + v32\_land\_missing(j2)\right) }{ m\_timestep\_length\_forestry } \cdot pc32\_yield\_forestry\_future(j2)\right) \leq \sum_{i2} pm\_demand\_forestry\_future(i2,"wood") \end{multline*}\]
Global minimum constraint based on a proportion (pc32_plant_prod_share_future) of future timber demand (pm_demand_forestry_future).
\[\begin{multline*} \sum_{j2}\left(\frac{ \left(\sum\left(ac\_est, v32\_land(j2,"plant",ac\_est)\right) + v32\_land\_missing(j2)\right) }{ m\_timestep\_length\_forestry } \cdot pc32\_yield\_forestry\_future(j2)\right) \geq \sum_{i2,ct}\left( pm\_demand\_forestry\_future(i2,"wood") \cdot s32\_plant\_share\right) \cdot \left(1-\sum_{ct}p32\_fix\_plant(ct)\right) \end{multline*}\]
Regional minimum constraint for maintaining current forestry area patterns, while accounting for regional self sufficiency in (pm_selfsuff_ext) timber production.
\[\begin{multline*} \sum_{cell(i2,j2)}\left( \left(\frac{\left(\sum\left(ac\_est, v32\_land(j2,"plant",ac\_est)\right) + v32\_land\_missing(j2)\right) }{ m\_timestep\_length\_forestry}\right) \cdot pc32\_yield\_forestry\_future(j2)\right) \geq pm\_demand\_forestry\_future(i2,"wood") \cdot s32\_plant\_share \cdot \sum_{ct} pm\_selfsuff\_ext(ct,i2,"wood") \cdot \left(1-\sum_{ct}p32\_fix\_plant(ct)\right) \end{multline*}\]
Extra investment costs
\[\begin{multline*} v32\_cost\_extra\_investment(j2) = \sum_{ac\_est} v32\_land(j2,"plant",ac\_est) \cdot \sum_{ct}pm\_investment\_layer(ct,j2) \cdot s32\_investment\_cost \end{multline*}\]
This constraint distributes additions to forestry land over ac_est, which depends on the time step length (e.g. ac0 and ac5 for a 10 year time step).
\[\begin{multline*} v32\_land(j2,type32,ac\_est) = \frac{ \sum_{ac\_est2} v32\_land(j2,type32,ac\_est2)}{card(ac\_est2)} \end{multline*}\]
Change in forestry area is the difference between plantation area from previous time step (‘pc32_land’) and optimized plantation area from current time step (‘v32_land’)
\[\begin{multline*} vm\_hvarea\_forestry(j2,ac\_sub) \leq v32\_land\_reduction(j2,"plant",ac\_sub) \end{multline*}\]
Certain areas (e.g. the boreal zone) are excluded from endogenous afforestation.
if(m_year(t) <= sm_fix_SSP2,
v32_land.fx(j,"aff","ac0") = 0;
else
v32_land.lo(j,"aff","ac0") = 0;
v32_land.up(j,"aff","ac0") = f32_aff_mask(j) * sum(land, pcm_land(j,land));
);No afforestation is allowed if carbon density <= 20 tc/ha
v32_land.fx(j,"aff","ac0")$(fm_carbon_density(t,j,"forestry","vegc") <= 20) = 0;Afforestation switch: 0 = Use natveg carbon densities for afforestation, 1 = Use plantation carbon densities for afforestation.
if(s32_aff_plantation = 0,
p32_carbon_density_ac(t,j,"aff",ac,ag_pools) = pm_carbon_density_ac(t,j,ac,ag_pools);
elseif s32_aff_plantation = 1,
p32_carbon_density_ac(t,j,"aff",ac,ag_pools) = pm_carbon_density_ac_forestry(t,j,ac,ag_pools);
);Timber plantations switch: 0 = Use natveg carbon densities for timber plantations, 1 = Use plantation carbon densities for timber plantations.
if(s32_timber_plantation = 0,
p32_carbon_density_ac(t,j,"plant",ac,ag_pools) = pm_carbon_density_ac(t,j,ac,ag_pools);
elseif s32_timber_plantation = 1,
p32_carbon_density_ac(t,j,"plant",ac,ag_pools) = pm_carbon_density_ac_forestry(t,j,ac,ag_pools);
);NDC carbon densities are natveg carbon densities.
p32_carbon_density_ac(t,j,"ndc",ac,ag_pools) = pm_carbon_density_ac(t,j,ac,ag_pools);CDR from afforestation for each age-class, depending on planning horizon.
p32_cdr_ac(t,j,ac)$(ord(ac) > 1 AND (ord(ac)-1) <= s32_planing_horizon/5)
= p32_carbon_density_ac(t,j,"aff",ac,"vegc") - p32_carbon_density_ac(t,j,"aff",ac-1,"vegc");CDR from timber plantations for each unharvested age-class.
p32_cdr_ac_plant(t,j,ac)$(ord(ac) > 1 AND ord(ac) < p32_rotation_cellular_harvesting(t,j))
= (p32_carbon_density_ac(t,j,"plant",ac,"vegc") - p32_carbon_density_ac(t,j,"plant",ac-1,"vegc")) * s32_plant_carbon_foresight;Regrowth of natural vegetation (natural succession) is modelled by shifting age-classes according to time step length. For first year of simulation, the shift is just 1. Division by 5 happends because the age-classes exist in 5 year steps
s32_shift = m_yeardiff_forestry(t)/5;Exchange land information after optimization
p32_land(t,j,type32,ac) = v32_land.l(j,type32,ac);Limitations Rotation lengths for timber plantations are not endogenous.
The static realisation is very simple and does not include any equation because forestry land is assumed constant at the observed 1995 level throughout time.
Costs and CDR from afforestation are set to zero.
vm_cost_fore.fx(i) = 0;
vm_cdr_aff.fx(j,ac,aff_effect) = 0;All forestry land pools (aff, ndc, plant) are fixed to zero, except forestry plantations, which are fixed to the level of 1995.
v32_land.fx(j,type32,ac) = 0;
v32_land.fx(j,"plant","acx") = pcm_land(j,"forestry");Forestry above ground carbon stocks are calculated by multiplying plantations in 1995 with the forestry above ground carbon density of the current time step (pc32_carbon_density).
pc32_carbon_density(j,ag_pools) = fm_carbon_density(t,j,"forestry",ag_pools);
vm_carbon_stock.fx(j,"forestry",ag_pools) =
sum((type32,ac), v32_land.l(j,type32,ac)*pm_carbon_density_ac(t,j,ac,ag_pools));Wood demand is also set to zero because forestry is not modeled in this realization.
vm_supply.fx(i2,kforestry) = 0;Limitations Forestry activities such as establishment or harvest of plantations for wood production are not modeled. Also afforestation for CDR is not included.
| Description | Unit | A | B | |
|---|---|---|---|---|
| f32_aff_bgp (j, bgp32) |
Biogeophysical temperature change of afforestation | \(degree C\) | x | |
| f32_aff_mask (j) |
afforestation mask | \(binary\) | x | |
| f32_aff_pol (t_all, j, pol32) |
npi+ndc afforestation policy | \(Mha new forest wrt to 2010\) | x | |
| f32_plant_prod_share (t_all) |
Share of overall production coming from plantations | \(1\) | x | |
| f32_tcre (j, tcre32) |
Transient surface temperature response to CO2 emission | \(degree C/tC/ha\) | x | |
| p32_aff_bgp (j, ac) |
Biophysical impact of afforestation | \(tCeq/ha\) | x | |
| p32_aff_pol (t, j) |
NDC forest stock | \(10^6 ha\) | x | |
| p32_aff_pol_timestep (t, j) |
NDC afforestation per time step | \(10^6 ha\) | x | |
| p32_aff_pot (t, j) |
Potential afforestation area | \(10^6 ha\) | x | |
| p32_aff_togo (t) |
Remaining exogenous afforestation wrt to the maximum exogenous target over time | \(10^6 ha\) | x | |
| p32_carbon_density_ac (t, j, type32, ac, ag_pools) |
Carbon density for ac and ag_pools | \(tC/ha\) | x | |
| p32_carbon_density_ac_forestry (t_all, j, ac) |
Above ground carbon density for age classes and carbon pools | \(tC/ha\) | x | |
| p32_carbon_density_ac_marg (t_all, j, ac) |
Marginal above ground carbon density for age classes and carbon pools | \(tC/ha\) | x | |
| p32_cdr_ac (t, j, ac) |
Non-cumulative CDR from afforestation plantations for each age-class depending on planning horizon | \(tC/ha\) | x | |
| p32_cdr_ac_plant (t, j, ac) |
Non-cumulative CDR from timber plantations for each age-class depending on planning horizon | \(tC/ha\) | x | |
| p32_discount_factor (t_all, j, ac) |
Discount factor for each age class | \(1\) | x | |
| p32_fix_plant (t_ext) |
Parameter deciding if plantation area shall be fixed after 2020 | \(1\) | x | |
| p32_IGR (t_all, j, ac) |
Instantaneous growth rate or periodic annual increment of forest growth | \(1\) | x | |
| p32_investment_returns_lost (t_all, j, ac) |
Present value of investment returns lost by not harvesting now and beginning a new series of rotations on the land | \(10^6 USD\) | x | |
| p32_land (t, j, type32, ac) |
Forestry land for each cell wood type and age class before and after optimization | \(10^6 ha\) | x | |
| p32_land_before (t, j, type32, ac) |
Saving time value of starting land | \(10^6 ha\) | x | |
| p32_land_rent_weighted (t_all, j, ac) |
Land rent weighted by the value of the trees at harvest age-class | \(10^6 USD\) | x | |
| p32_land_start_ac (j, type32, ac) |
Saving first value of starting land | \(10^6 ha\) | x | |
| p32_max_aff_area | Maximum global afforestation area that is greater or equal the exogenous policy target | \(10^6 ha\) | x | |
| p32_ncells (i) |
Number of cells in each region | \(1\) | x | |
| p32_net_present_value (t_all, j, ac) |
Net present value for a representative 1ha land of plantations | \(10^6 USD\) | x | |
| p32_plant_ini_ac (j) |
Initialization of plantation area | \(10^6 ha\) | x | |
| p32_rot_flg (t_all, j, ac) |
Identifier flag when calculating rotation length | \(1\) | x | |
| p32_rot_flg_faustmann (t_all, j, ac) |
Identifier flag when calculating faustmann rotation length | \(1\) | x | |
| p32_rot_length_ac_eqivalent (t_all, j) |
Cellular rotation length of plantations translated to age class equivalent for future | \(1\) | x | |
| p32_rot_length_faustmann (t_all, j) |
Cellular Faustmann rotation length of plantations translated to age class equivalent | \(1\) | x | |
| p32_rotation_cellular_estb (t_all, j) |
Establishment rotation length translated to age classes on cellular level | \(1\) | x | |
| p32_rotation_cellular_harvesting (t_all, j) |
Harvesting rotation length of plantations translated to age class equivalent for future | \(1\) | x | |
| p32_rotation_offset | Offset calc in age class equivalents | \(1\) | x | |
| p32_rotation_regional (t_all, i) |
Regional average rotation length of plantations translated to age class equivalent for future | \(1\) | x | |
| p32_stand_value (t_all, j, ac) |
Stand value based on given prices | \(10^6 USD\) | x | |
| p32_tcre_glo (j) |
Global mean Transient Climate Response to cumulative Emissions | \(degree C/tC/ha\) | x | |
| p32_time (ac) |
Time as a function of age-classes | \(yr\) | x | |
| pc32_carbon_density (j, ag_pools) |
Above ground carbon density in optimization | \(tC/ha\) | x | |
| pc32_land (j, type32, ac) |
Forestry land per forestry land type initialization of the optimization | \(10^6 ha\) | x | |
| pc32_yield_forestry_future (j) |
Cellular timber yield expected in the future | \(m3/ha/year\) | x | |
| q32_aff_est (j) |
Afforestation constraint for establishment age classes | \(10^6 ha\) | x | |
| q32_aff_pol (j) |
Afforestation policy constraint | \(10^6 ha\) | x | |
| q32_bgp_aff (j, ac) |
Biophysical afforestation calculation | \(10^6 tCeq\) | x | |
| q32_carbon (j, ag_pools) |
Forestry carbon stock calculation | \(10^6 tC\) | x | |
| q32_cdr_aff (j, ac) |
Calculation of CDR from afforestation | \(10^6 tC\) | x | |
| q32_cost_establishment (i) |
Present value of cost of establishment | \(10^6 USD\) | x | |
| q32_cost_extra_investment (j) |
Extra investment needed for establishing plantations in unproductive areas | \(10^6 USD\) | x | |
| q32_cost_recur (i) |
Recurruing costs | \(10^6 USD\) | x | |
| q32_cost_total (i) |
Total forestry costs constraint | \(10^6 USD\) | x | |
| q32_establishment_max_glo | Establishment in current time step for future demand | \(10^6 ha\) | x | |
| q32_establishment_min_glo | Establishment in current time step for future demand | \(10^6 ha\) | x | |
| q32_establishment_min_reg (i) |
Establishment in current time step for future demand | \(10^6 ha\) | x | |
| q32_fix_plant_area (j) |
Fixation of cellular plantation area based on area fix switch | \(10^6 ha\) | x | |
| q32_forestry_est (j, type32, ac) |
Distribution of forestry establishment over ac_est | \(10^6 ha\) | x | |
| q32_hvarea_forestry (j, ac) |
Plantations area harvest | \(10^6 ha\) | x | |
| q32_land (j) |
Land constraint | \(10^6 ha\) | x | |
| q32_land_diff | Aggregated difference in forestry land compared to previous timestep | \(10^6 ha\) | x | |
| q32_land_expansion (j, type32, ac) |
Land expansion | \(10^6 ha\) | x | |
| q32_land_reduction (j, type32, ac) |
Land contraction | \(10^6 ha\) | x | |
| q32_max_aff | Maximum total global afforestation | \(10^6 ha\) | x | |
| s32_aff_plantation | Switch for using growth curves for afforestation 0=natveg 1=plantations | \(1\) | x | |
| s32_faustmann_rotation | Switch to activate faustmann rotations | \(1\) | x | |
| s32_fix_plant | Fixing plantation area after sm_fix_SSP2 0=Not fixed 1=Fixed | \(1\) | x | |
| s32_forestry_int_rate | Global interest rate for plantations | \(percent\) | x | |
| s32_free_land_cost | Very high cost for using non existing land for plantation establishment | \(USD/ha\) | x | |
| s32_harvesting_cost | Harvesting cost | \(USD/ha\) | x | |
| s32_initial_distribution | Switch to Activate ageclass distribution in plantations 1=on 0=off | \(1\) | x | |
| s32_investment_cost | Additional investment cost in plantations | \(USD/tC/ha\) | x | |
| s32_max_aff_area | Maximum total global afforestation | \(10^6 ha\) | x | |
| s32_planing_horizon | Afforestation planing horizon | \(years\) | x | |
| s32_plant_carbon_foresight | Switch to allow plantations to be used as incentives for CDR | \(1\) | x | |
| s32_plant_share | Constant percentage of production which can come from plantations | \(1\) | x | |
| s32_price | Price for timber | \(USD\) | x | |
| s32_recurring_cost | Recurring costs | \(USD/ha\) | x | |
| s32_recurring_cost_multiplier | Cost multiplier for recurring costs only for testing | \(1\) | x | |
| s32_reESTBcost | Re establishment cost | \(USD/ha\) | x | |
| s32_rotation_extension | Rotation extension factor 1=original rotations 2=100 percent increase in rotations etc | \(1\) | x | |
| s32_shift | Number of 5-year age-classes corresponding to current time step length | \(1\) | x | |
| s32_tcre_local | Switch for local (1) or global (0) TRCE factors | \(1\) | x | |
| s32_timber_plantation | Switch for using growth curves for timber plantations 0=natveg 1=plantations | \(1\) | x | |
| v32_cost_establishment (i) |
Cost of establishment calculated at the current time step | \(10^6 USD\) | x | |
| v32_cost_extra_investment (j) |
Extra investment needed for establishing plantations in unproductive areas | \(10^6 USD\) | x | |
| v32_cost_recur (i) |
Recurring forest management costs | \(USD/ha\) | x | |
| v32_land (j, type32, ac) |
Forestry land pools | \(10^6 ha\) | x | x |
| v32_land_expansion (j, type32, ac) |
Forestry land expansion | \(10^6 ha\) | x | |
| v32_land_missing (j) |
Forestry land which can be used at extrmemly high costs in case not enough area is available for new establishment | \(10^6 ha\) | x | |
| v32_land_reduction (j, type32, ac) |
Forestry land reduction | \(10^6 ha\) | x | x |
| description | |
|---|---|
| ac | Age classes |
| ac_bph(ac) | fade-in of bph effect over age-classes |
| ac_est(ac) | Dynamic subset of age classes for establishment |
| ac_sub(ac) | Dynamic subset of age classes excluding establishment |
| aff_effect | biochemical and local biophysical effect of afforestation on climate |
| ag_pools(c_pools) | Above ground carbon pools |
| age | Population age groups |
| bgp32 | biogeophysical effect (degree C) of afforestation on local surface temperature |
| c_pools | Carbon pools |
| cell(i, j) | number of LPJ cells per region i |
| ct(t) | Current time period |
| fcosts32(fcostsALL) | forestry factor cost per annum |
| fcostsALL | forestry factor cost types |
| forest_land(land) | land from which timber can be taken away |
| i | all economic regions |
| i2(i) | World regions (dynamic set) |
| ini32(j, ac) | subset for initialization of timber plantations |
| j | number of LPJ cells |
| j2(j) | Spatial Clusters (dynamic set) |
| kall | All products in the sectoral version |
| kforestry(k) | forestry products |
| land | Land pools |
| pol32 | afforestation policy type |
| rotation_type | Rotation type |
| t_all(t_ext) | 5-year time periods |
| t_ext | 5-year time periods |
| t_future(t_all) | 5-year time periods |
| t_historical(t_all) | Historical period |
| t(t_all) | Simulated time periods |
| tcre32 | transient surface temperature response to CO2 emission (degree C per tC) |
| type | GAMS variable attribute used for the output |
| type32 | plantation type |
Florian Humpenöder, Abhijeet Mishra
10_land, 11_costs, 12_interest_rate, 14_yields, 16_demand, 21_trade, 52_carbon, 56_ghg_policy, 73_timber
Amacher, Gregory S, Markku Ollikainen, and Erkki Koskela. 2009. Economics of Forest Resources. Mit Press Cambridge.
Braakhekke, Maarten C., Jonathan C. Doelman, Peter Baas, Christoph Müller, Sibyll Schaphoff, Elke Stehfest, and Detlef P. van Vuuren. 2019. “Modelling Forest Plantations for Carbon Uptake with the LPJmL Dynamic Global Vegetation Model.” Earth System Dynamics Discussions, April, 1–24. https://doi.org/https://doi.org/10.5194/esd-2019-13.
Humpenöder, Florian, Alexander Popp, Jan Philip Dietrich, David Klein, Hermann Lotze-Campen, Markus Bonsch, Benjamin Leon Bodirsky, Isabelle Weindl, Miodrag Stevanovic, and Christoph Müller. 2014. “Investigating Afforestation and Bioenergy CCS as Climate Change Mitigation Strategies.” Environmental Research Letters 9 (6): 064029. https://doi.org/10.1088/1748-9326/9/6/064029.
Sathaye, Jayant, Willy Makundi, Larry Dale, Peter Chan, and Kenneth Andrasko. 2005. “GHG Mitigation Potential, Costs and Benefits in Global Forests: A Dynamic Partial Equilibrium Approach.” Lawrence Berkeley National Laboratory, March. http://escholarship.org/uc/item/92d5m16v.